Mathematical Methods for Data Analysis 学习笔记(2) Decision Analysis

2019-09-24 20:43

学习笔记 

3259 阅读

0 回复

Vacabulary for this chapter
optimal strategy 最优策略
mutually exclusive 互相排斥的（相互独立）
collectively exhaustive 完全穷尽
optimistic 乐观的
conservative 保守的
chronological 按（时间）先后顺序的
sensitivity 灵敏度
prior probability 先验概率
posterior probability 后验概率

Problem Formulation

The decision alternatives are the different possible strategies the decision maker can employ.
The states of nature refer to future events, not under the control of the decision maker, which may occur. States of nature should be defined so that they are mutually exclusive and collectively exhaustive.

Influence Diagrams (影响图)

An influence diagram is a graphical device showing the relationships among the decisions, the chance events, and the consequences.

• Squares or rectangles depict decision nodes. 正方形或矩形表示决策节点。
• Circles or ovals depict chance nodes. 圆形或椭圆形表示机会节点。
• Diamonds depict consequence nodes. 菱形表示结果节点。
• Lines or arcs connecting the nodes show the direction of influence. 连接节点的线或弧表示影响的方向。

Payoff Tables (收益表)

The consequence resulting from a specific combination of a decision alternative and a state of nature is a payoff.

A table showing payoffs for all combinations of decision alternatives and states of nature is a payoff table.

Payoffs can be expressed in terms of profit, cost, time, distance or any other appropriate measure.

Payoff table example (payoffs in $ millions):

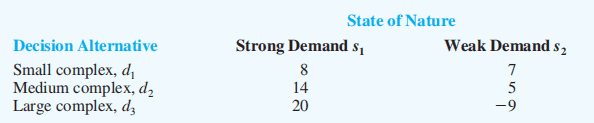
Decision Making without Probabilities

Three commonly used criteria for decision making when probability information regarding the likelihood of the states of nature is unavailable are:

• the optimistic approach 乐观方法
• the conservative approach 保守方法
• the minimax regret approach. 极小极大后悔方法

Optimistic Approach

The optimistic approach would be used by an optimistic decision maker.

The decision with the largest possible payoff is chosen.

If the payoff table was in terms of costs, the decision with the lowest cost would be chosen.

In the above example, maximum payoff for each decision alernative:

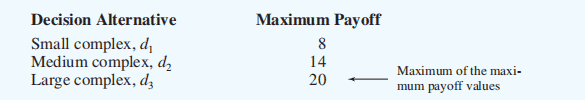
We choose the decision that has the largest single value in the payoff table ($d_{3}$)。

Conservative Approach

The conservative approach would be used by a conservative decision maker.

For each decision the minimum payoff is listed and then the decision corresponding to the maximum of these minimum payoffs is selected. (Hence, the minimum possible payoff is maximized.)

If the payoff was in terms of costs, the maximum costs would be determined for each decision and then the decision corresponding to the minimum of these maximum costs is selected. (Hence, the maximum possible cost is minimized.)

Minimax Regret Approach

The minimax regret approach requires the construction of a regret table or an opportunity loss table.
This is done by calculating for each state of nature the difference between each payoff and the largest payoff (最大的 payoff 与每一个 payoff 的差) for that state of nature.
Then, using this regret table, the maximum regret for each possible decision is listed. （取每一个 decision 的最大值）

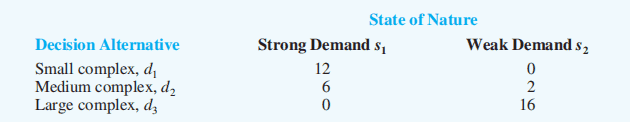
The decision chosen is the one corresponding to the minimum of the maximum regrets. （所有 maximum regret 中的最小值）

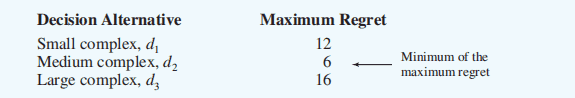
Decision Making with Probabilities

Expected Value Approach（期望值法）

If probabilistic information regarding the states of nature is available, one may use the expected value (EV) approach.

Here the expected return for each decision is calculated by summing the products of the payoff under each state of nature and the probability of the respective state of nature occurring.

The decision yielding the best expected return is chosen.

The expected value of a decision alternative is the sum of weighted payoffs for the decision alternative.

$P\left(s_{j}\right) \geq 0 \quad \text { for all states of nature }$

$\sum_{j=1}^{N} P(s)=P\left(s_{1}\right)+P\left(s_{2}\right)+\cdots+P\left(s_{N}\right)=1$

The expected value (EV) of decision alternative di is defined as:

$\mathrm{EV}\left(d_{i}\right) = \sum_{j=1}^{N} P\left(s_{j}\right) V_{i j}$

Where:
N = the number of states of nature
$P\left(s_{j}\right)$ = the probability of state of nature $S_{j}$
$V_{i j}$ = the payoff corresponding to decision alternative $d_{i}$ and state of nature $S_{j}$

Decision Tree（决策树）

A decision tree is a chronological representation of the decision problem.

Each decision tree has two types of nodes; round nodes correspond to the states of nature while square nodes correspond to the decision alternatives. 圆形节点对应于自然状态，而方形节点对应于决策选择。
The branches leaving each round node represent the different states of nature while the branches leaving each square node represent the different decision alternatives.

At the end of each limb of a tree are the payoffs attained from the series of branches making up that limb.

Decision tree with state-of-nature branch probabilities:

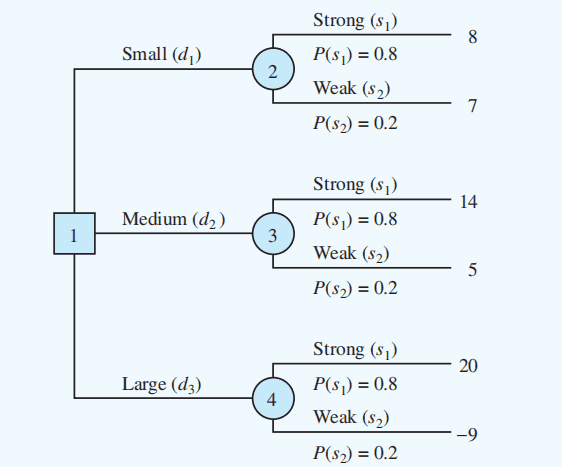
Applying the expected value approach using a decision tree:

根据决策树计算期望值。
Choose the decision alternative with the largest EV. 所以上图选择 $d_3$，因为 14.2 最大。

Expected Value of Perfect Information

In general, the expected value of perfect information (EVpi) is computed as follows:

$\text { EVPI }=| \text { EVwPI }-\text { EVwoPI } |$

where
EVPI = expected value of perfect information
EVwPI = expected value with perfect information about the states of nature
EVwoPI = expected value without perfect information about the states of nature

For example:
EVwPI = .8(20 mil) + .2(7 mil) = $17.4 mil
EVwoPI = .8(20 mil) + .2(-9 mil) = $14.2 mil
EVPI = |EVwPI – EVwoPI| = |17.4 – 14.2| = $3.2 mil

Risk Analysis and Sensitivity Analysis

Risk Analysis（风险分析）

Risk analysis helps the decision maker recognize the difference between:

• the expected value of a decision alternative, and
• the payoff that might actually occur

The risk profile for a decision alternative shows the possible payoffs for the decision alternative along with their associated probabilities.

Large Complex Decision Alternative:

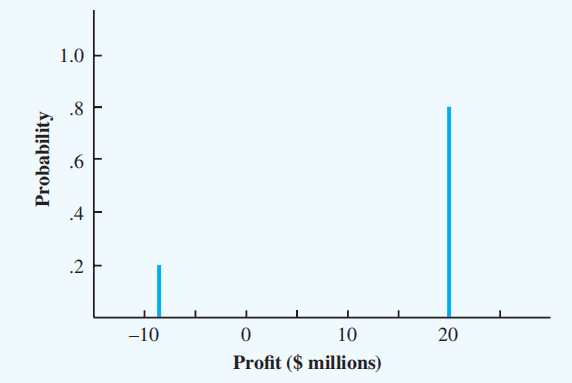
Sensitivity Analysis（敏感性分析）

Sensitivity analysis can be used to determine how changes to the following inputs affect the recommended decision alternative:

• probabilities for the states of nature
• values of the payoffs

If a small change in the value of one of the inputs causes a change in the recommended decision alternative, extra effort and care should be taken in estimating the input value.

Decision Analysis with Sample Information

Frequently, decision makers have preliminary or prior probability (先验概率) assessments for the states of nature that are the best probability values available at that time.

To make the best possible decision, the decision maker may want to seek additional information about the states of nature.

This new information, often obtained through sampling, can be used to revise the prior probabilities so that the final decision is based on more accurate probabilities for the states of nature.

These revised probabilities are called posterior probabilities (后验概率).

Influence Diagram

Influence diagram with sample information:

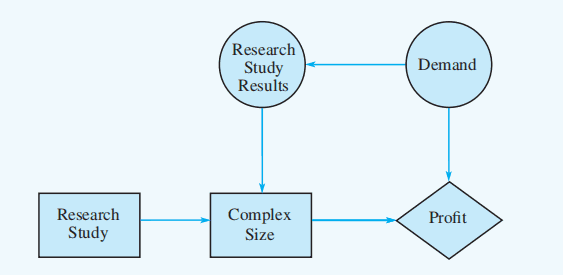
Sample Information

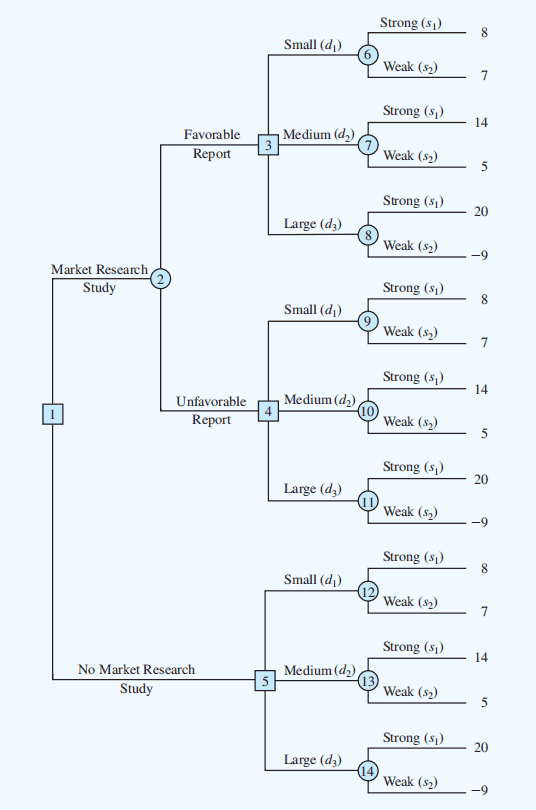
If the market research study is undertaken

$\begin{array}{c}{P(\text { Favorable report })=0.77} \\ {P(\text { Unfavorable report })=0.23}\end{array}$

If the market research report is favorable

$\begin{array}{l}{P(\text { Strong demand given a favorable report })=0.94} \\ {P(\text { Weak demand given a favorable report })=0.06}\end{array}$

If the market research report is unfavorable

$\begin{array}{l}{P(\text { Strong demand given an unfavorable report })=0.35} \\ {P(\text { Weak demand given an unfavorable report })=0.65}\end{array}$

If the market research report is not undertaken, the prior probabilities are applicable.

$\begin{aligned} P(\text { Strong demand }) &=0.80 \\ P(\text { Weak demand }) &=0.20 \end{aligned}$

The branch probabilities are shown on the decision tree:

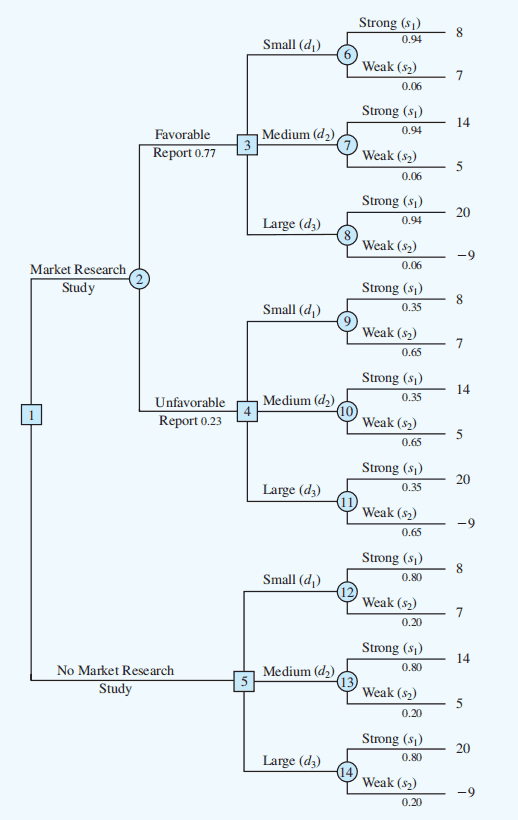
Decision Strategy (决策策略)

A decision strategy is a sequence of decisions and chance outcomes where the decisions chosen depend on the yet-to-be-determined outcomes (尚未确定的结果) of chance events.

The approach used to determine the optimal decision strategy is based on a backward pass through the decision tree using the following steps:

• At chance nodes, compute the expected value by multiplying the payoff at the end of each branch by the corresponding branch probabilities.
• At decision nodes, select the decision branch that leads to the best expected value. This expected value becomes the expected value at the decision node.

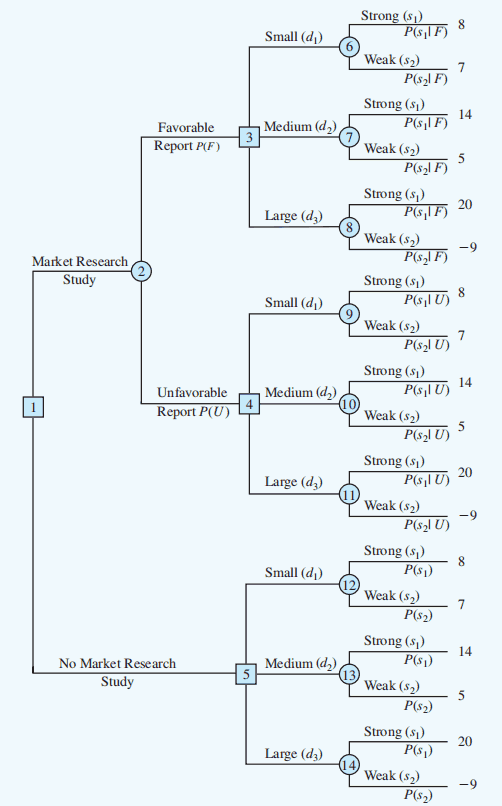
In the PDC example, decision tree after computing expected values at chance nodes 6 to 14

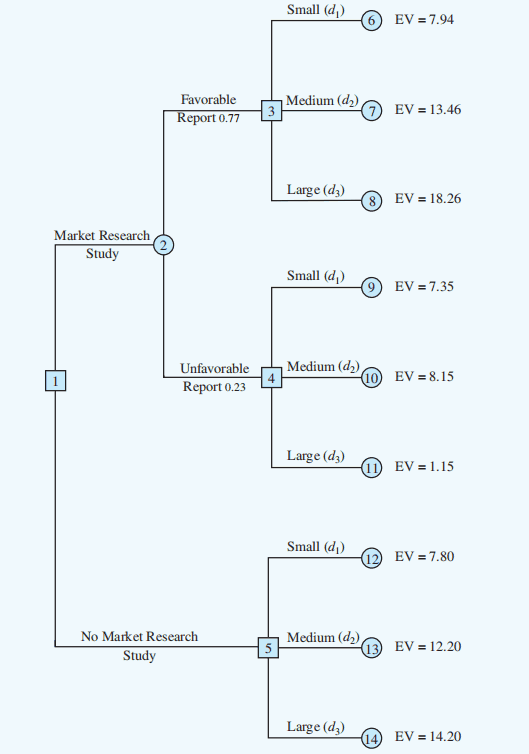
Decision tree after choosing best decisions at nodes 3:

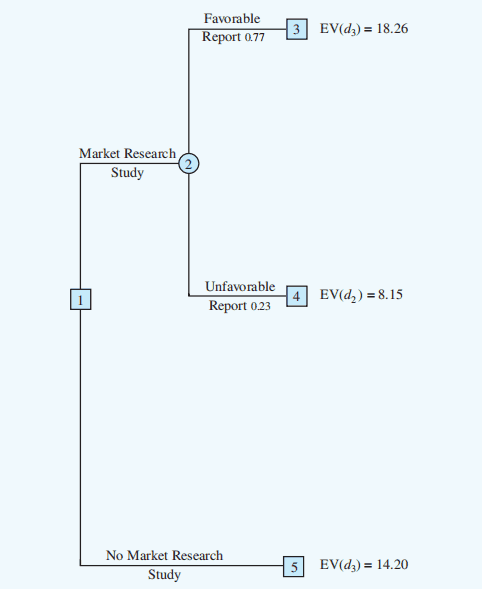
Decision tree reduced to two decision branches:

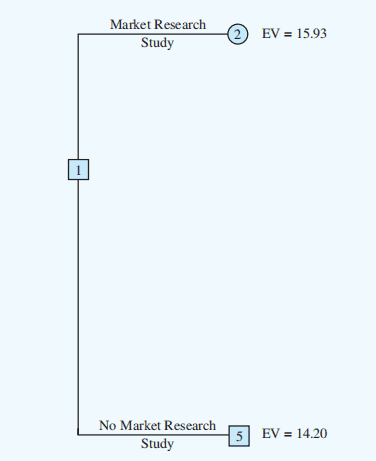
Finally, the decision can be made at decision node 1 by selecting the best expected val ues from nodes 2 and 5. This action leads to the decision alternative to conduct the market research study, which provides an overall expected value of 15.93.

The optimal decision for PDC is to conduct the market research study and then carry out the following decision strategy:

• If the market research is favorable, construct the large condominium complex.
• If the market research is unfavorable, construct the medium condominium complex.

Expected Value of Sample Information

The expected value of sample information (EVSI) is the additional expected profit possible through knowledge of the sample or survey information.

The expected value associated with the market research study is $15.93.

The best expected value if the market research study is not undertaken is $14.20.

We can conclude that the difference, $15.93 - $14.20 = $1.73, is the expected value of sample information.

Conducting the market research study adds $1.73 million to the PDC expected value.

Efficiency of Sample Information

Efficiency of sample information is the ratio of EVSI to EVPI.

$\mathrm{E}=\frac{\mathrm{EVSI}}{\mathrm{EVPI}} \times 100$

For the PDC problem,

$\mathrm{E}=\frac{1.73}{3.2} \times 100=54.1 \%$

As the EVPI provides an upper bound for the EVSI, efficiency is always a number between 0 and 1.

Computing Branch Probabilities (计算分支概率)

We will need conditional probabilities for all sample outcomes given all states of nature, that is, $P\left(F | s_{1}\right)$, $P\left(F | s_{2}\right)$, $P\left(U | s_{1}\right)$, and $P\left(U | s_{2}\right)$.

And the decision tree for the sample is:

Branch (Posterior) Probabilities Calculation (分支（后验）概率计算)

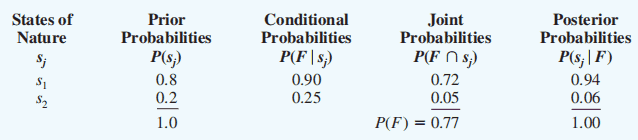
• Step 1:For each state of nature, multiply the prior probability by its conditional probability for the indicator – this gives the joint probabilities (联合概率) for the states and indicator.
• Step 2: Sum these joint probabilities over all states – this gives the marginal probability (边际概率) for the indicator.
• Step 3: For each state, divide its joint probability by the marginal probability for the indicator – this gives the posterior probability distribution.

Bayes’Theorem and Posterior Probabilities

Knowledge of sample (survey) information can be used to revise the probability estimates for the states of nature.

Prior to obtaining this information, the probability estimates for the states of nature are called prior probabilities.

With knowledge of conditional probabilities for the outcomes or indicators of the sample or survey information, these prior probabilities can be revised by employing Bayes’ Theorem.

The outcomes of this analysis are called posterior probabilities (后验概率) or branch probabilities (分支概率) for decision trees.

Branch probabilities for the PDC example based on a favorable market research report:

Branche probabilities for the PDC example based on an unfavorable market research report:

BAYES’ THEOREM (贝叶斯定理)

BAYES’ THEOREM:

$P\left(A_{i} | B\right)=\frac{P\left(B | A_{i}\right) P\left(A_{i}\right)}{\sum_{j} P\left(B | A_{j}\right) P\left(A_{j}\right)}$